
(immagine tratta dal sito "lofficina.eu" Esiste un sistema per determinare la lunghezza focale degli obiettivi di un binocolo senza dover rimuovere gli stessi dal corpo centrale? Questa la domanda postami da un astrofilo qualche tempo fa, motivata evidentemente più da curiosità che da interesse pratico, in quanto i parametri fondamentali di un binocolo che ogni osservatore dovrebbe conoscere sono essenzialmente due: il diametro dell'obiettivo e gli ingrandimenti, prescindendo pertanto da dove si forma effettivamente l'immagine dell'oggetto. Tra l'altro, svitare un obiettivo dallo scafo del binocolo è una operazione che in primo luogo non è sempre possibile, dal momento che esistono binocoli (come lo storico BWCF 20x80 in auge negli anni '80 e '90) che sono a corpo unico. In secondo luogo, rimuovere un obiettivo non è mai una cosa raccomandabile, specialmente se fatta da una persona inesperta, perché le parti rifrangenti interne (lenti e prismi) sarebbero facilmente alla mercé del pulviscolo e/o di altre sostanze in sospensione nell'aria, che una volta depositatesi potrebbero compromettere la qualità dell'immagine.
L'unico mezzo efficace per raggiungere il nostro scopo è allora costituito dalla matematica che nella fattispecie si riduce a qualche operazione algebrica e a una semplice equazione di II grado che ogni studente liceale è in grado di risolvere.
Cominciamo dunque col considerare la formula delle lenti — reperibile in qualunque testo di ottica — supponendo, per semplificare il discorso, che il doppietto acromatico del binocolo sia in realtà costituito da una sola lente avente le stesse caratteristiche risultanti:
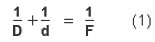
Questa celebre formula esprime una relazione molto semplice fra 3 grandezze:
- D = distanza alla quale si trova l'oggetto inquadrato;
- d = distanza dal centro ottico dell'obiettivo alla quale si forma l'immagine reale (capovolta) dell'oggetto inquadrato;
- F = lunghezza focale dell'obiettivo.
d = F ![]()
quindi l'immagine viene a cadere nel piano focale dell'obiettivo.
Delle tre grandezze che compaiono nella (1) l'unica che può essere determinata facilmente è solo la prima, misurando letteralmente la distanza tra il binocolo (che dovrà essere montato su un treppiede) e l'oggetto inquadrato che verrà scelto a distanza di pochi metri, nel caso che l'esperimento venga condotto in casa, o al massimo qualche decina di metri, nel caso ci si trovasse, ad esempio, in un giardino o in un parco.
Se è vero che dalla (1) non si può determinare direttamente né d né F, è però possibile trovare con una certa precisione
la differenza d - F: basterà misurare di quanto gli oculari dei binocolo vanno estratti per la rimessa a fuoco quando da un oggetto situato distanza molto grande (D = infinito) si passa a osservarne uno di cui è possibile determinare la distanza. In altri termini, si avrà:
d − F = k![]() (2)
(2)
ove k è una costante che dipenderà dalla distanza D dell'oggetto precedentemente stabilita. Misurando il numero di giri (e/o frazioni di giro) che deve compiere la ruota zigrinata del focheggiatore centrale per estrarre gli oculari, in modo da focheggiare l'immagine dell'oggetto posto a distanta finita, è possibile determinare k con una precisione anche di una frazione di millimetro! A questo punto non si dovrà fare altro che combinare la (1) con la (2), ottenendo un sistema di 2 equazioni nelle 2 incognite d ed F, che ci apprestiamo a risolvere.
Dalla (2) risistemando i termini si ricava:
d = F + k![]()
che, sostituita nella (1), dopo semplici passaggi algebrici che per brevità omettiamo, ci conduce all'espressione:
F2 + Fk − Dk = 0
![]()
Questa è un'equazione di secondo grado nella variabile F avente, come noto, due soluzioni. Una, però, è negativa ed è evidentemente da scartare perché non avrebbe alcun senso (una lente o, in generale, un sistema positivo di lenti come quelli presenti negli obiettivi astronomici e fotografici non può avere focale negativa!). Il valore di F ricavato dalla (3) è pertanto:

Nel caso dei telescopi newtoniani, nei quali, contrariamente ai binocoli, è nota la lunghezza focale dell'obiettivo, può essere curioso applicare lo stesso procedimento per determinare la distanza di un oggetto senza ricorrere a sistemi trigonometrici. Basterà ricavare dalla (4) il valore di D, ricordandosi sempre di misurare k con la massima precisione possibile, poiché per bersagli lontani parecchie centinaia di metri, o addirittura alcuni chilometri, l'escursione che deve compiere il focheggiatore è minima. In questo caso sarà:

Non sto adesso a dilungarmi in esempi che potrebbero appesantire inutilmente la lettura; mi limito soltanto a rammentare un paio di cose. La prima è che la (1) così come è scritta non si può applicare agli Schmidt-Cassegrain, perché in questi telescopi la messa a fuoco avviene spostando avanti e indietro lo specchio principale. Se quest'operazione non introduce alcuna novità nel caso di un Newton, il discorso cambia in un Cassegrain, perché essendo lo specchietto secondario non piano ma iperbolico, a ogni escursione del focheggiatore si avrebbe una sia pur debole variazione della focale equivalente; la (5) risulterebbe pertanto valida solo in prima approssimazione. La seconda (sarà spero superflua) riguarda le grandezze che compaiono nelle varie espressioni, le quali devono essere espresse tutte nella stessa unità di misura; questo per evitare che una volta fatte le debite misurazioni e i calcoli col massimo scrupolo si giunga a risultati affatto incongruenti!

